Knight's Tour (Math Lair)

Math Lair Home > Topics > Knight's Tour

The Knight's move in chess is L-shaped, being two squares in one direction and one in a perpendicular direction. For example, A Knight positioned as shown can move to any of the eight squares marked with an orange dot.

A chess-related problem dating to at least 300 years ago is to find a sequence of moves of a knight on a chessboard such that the knight visits each square on the chessboard exactly once. Such a sequence is called a knight's tour. Famous mathematicians such as De Moivre, Euler, and Vandermonde have written about this problem.

A knight's tour can be closed, which means that the knight ends up one move away from the beginning square, or open, which means that the knight ends up somewhere else.

While there are many different ways to create a knight's tour, doing so can be a challenge. There are several heuristics that are. One such heuristic is to visit squares closer to the outer ring of the board first. Another one is that, whenever you have a choice of squares, move the knight to the square having the fewest number of possible moves out of that square. If you're trying to create a closed magic squre, you need to be careful of the corner squares; there are only two knight moves out of a corner square, so you have to be careful not to land on those squares unless you have just moved the knight out of the corner or you are about to do so. If you get stuck before you cover all 64 squares, it can help to backtrack and try different paths.

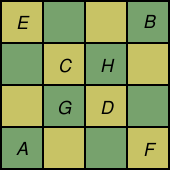It is also interesting to investigate on what sizes of board a knight's tour is possible. It's easy to see that a knight's tour is impossible on a 3×3 board, because the middle square cannot be reached. Is a knight's tour possible on a 4×4 board? As it turns out, it isn't possible. Take a look at the image on the right. The only way to get in and out of square A is through squares C and D, and the only way to get in and out of square B is also through squares C and D. So, a knight's tour is impossible unless it starts at either A or B and ends elsewhere (or vice versa). So, such a tour could start A–C–B–D... Now, consider squares E and F. They have the same problem as squares A and B. So, our knight's tour would have to end on one of them; one possibility is ...G–F–H–E. So, the remaining eight squares must be in the middle, but there is no path that connects those eight squares to each other and only each other. It can be shown that an open tour is possible on any board 5×5 or greater. You may want to investigate other squares and rectangles to see under what conditions open or closed knight's tours are possible.