Magic Squares

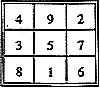
A magic square is an arrangement of numbers in a square such that all rows, all columns, and both main diagonals sum to the same number, a number referred to as the magic constant. The square on the right is perhaps the best-known example of a magic square. Magic squares are a very well-known mathematical recreation.

Terminology

A normal magic square is a type of magic square that contains each of the numbers between 1 and n² (where n is the side length of the square). For example, the magic square above, which is a 3×3 magic square containing the numbers 1 through 9, is a normal magic square.

A symmetrical magic square is a magic square for which the sum of any two numbers located symmetrically around the centre of the magic square is always the same.

A pandiagonal magic square is one for which the broken diagonals also sum to the magic constant.

Semimagic (or semi-magic) squares are squares whose rows and columns sum to the same sum, but whose main diagonals do not.

The order of a magic square is the length of one of its sides.

The magic constant is the sum of one row, column, or diagonal. For a normal magic square, it is equal to ½n(n² + 1).

History

The Arabs seem to have been the first people to study magic squares (called wafq in Arabic) extensively, although they weren't the first to know about them; Chinese mathematicians knew about them several centuries earlier, and they appear in the I Ching. The first appearance in Islamic literature is found in the writings of Jabir ibn Hayyan, known in Europe as Geber, who wrote around the end of the 9th or the start of the 10th century.

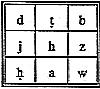
Geber attributed medicinal or mystical properties to the magic square, which is why magic squares are called "magic squares". He wrote the numbers of the magic square using the abjad numerals (not Hindu-Arabic numerals).

In subsequent years Islamic writers developed a variety of methods for forming larger magic squares in which no numeral was repeated. and the sums of each row and each column and the two diagonals were the same. By the year 983, they had discovered magic squares of size 5×5 and 6×6. By the 13th century, 10×10 squares were being produced.

The first European author who appears to have written about magic squares from a mathematical perspective was Emanuel (or Manuel) Moschopulus, around the start of the fourteenth century or so. Christian Europe, like the Muslim nations, was also interested in the supposed mystical properties of magic squares; in the sixteenth century the astrologer Cornelius Agrippa constructed magic squares of orders 3 through 9, which he associated with the seven astrological "planets", and associated a square of size 1, containing just the number 1, with the unity of God, and asserted that the fact that no normal magic square of order 2 existed illustrated the imperfection of the physical world.

A famous appearance of a magic square is in Albrecht Dürer's engraving Melencolia I (sometimes referred to as Melancholia). A 4×4 magic square appears in the upper right-hand corner of the work; the two numbers in the middle columns of the bottom row are 15 and 14, representing the year that the engraving was created, 1514. This picture is very commonly seen in works about magic squares, the authors of these works perhaps being unaware that the theme of the engraving is that study leads to melancholy and frustration!

A few centuries later, magic squares were no longer created for their supposed magical or mystical properties; rather, they were studied as a recreation. In the 18th century, Benjamin Franklin passed some of his free time creating magic squares, creating 8×8 and 16×16 semi-magic squares with curious properties. Meanwhile, in Russia, the Swiss mathematician Euler constructed an 8×8 semi-magic square that corresponded to a knight's tour on a chessboard. By the 19th century 100×100 magic squares, with 10,000 individual cells, were being produced.

Constructing a Magic Square

The following describes how to construct natural magic squares (with numbers from 1 to n²). To construct other magic squares, construct a natural magic square and then see "Properties of Magic Squares", below).

There are several methods of constructing magic squares. Different methods are used depending on whether the order of the magic square is odd, singly even (divisible by two but not by four) or a multiple of four:

Magic squares with an odd side length can be constructed as follows:

Place all numbers in the square in numerical order, as follows:

• Start in the square beneath the square in the centre (so 1 would go in this square).
• Each successive number goes one square below and one square to the right of the previous number. Think of the square as wrapping around on itself from top to bottom so, for example, if you placed a number in the bottom right corner, the next number would be placed in the top left corner.
• If there is a number already occupying the square for which you want to put the next number, place the next number two steps below the previous number, in the same column.

See the magic square at the right for an example of the process. The above method is called the Barcet de Méziriac method.

Another way of creating an odd-order magic square (called De la Loubère's rule) is as follows. It consists of starting with the number 1 in the middle cell of the top row. Each successive number goes one square above and one square to the right of the previous number. As above, think of the square as wrapping around on itself. If you are blocked, place the next number one step below the previous number, in the same column.

Doubly-even-order magic squares (magic squares whose side length is divisible by 4) can be created as follows:

• Write the numbers 1 through n² (where n is the side length) in their natural order, as shown on the right.
• If the square length is 8 or more, divide the square into 4×4 sub-squares.
• In each of the 4×4 sub-square, take each number along the main diagonals (highlighted in the example on the right, and replace it with the number that you would have to add to it to sum to n² + 1. For example, in the order-4 magic square on the right, 1 would be replaced by 16, 4 by 13, and so on.

The result is shown on the right. Magic squares constructed in this manner also have the property that they are symmetric.

Singly-even-order magic squares (magic squares whose side length is divisible by 2 but not 4) can be created as follows:

• A	C
  D	B

  Divide the square into four equal quadrants, labelled A, B, C, and D in the diagram at the right. Note the placement of the labels. These four quadrants will have an odd side length.
• In each of A, B, C, and D, construct a magic square using De la Loubère's rule.
• Calculate two values, which we'll call u and m. u is simply the order of the smaller squares. To calculate m, take u, subtract 1, and divide it by 2. So, for example, if you are constructing a magic square of order 6, u will be 3, and m will be equal to 1.
• Add u² to each value in B. Add 2u² to each value in C. Add 3u² to each value in D.
• In the middle row of A, take the m cells starting at the second column, and interchange the numbers with the corresponding cells in D. In every other row of A, take the m cells starting at the first column, and interchange the numbers with the corresponding cells in D.
• Interchange the cells in the m − 1 columns of C with the corresponding cells in D. (in the example constructing a magic square of order 6, m − 1 = 0, so no interchanging is done).

The result will be a magic square, as shown on the left.

Once you have a normal magic square, there are several operations that you can use to turn it into a non-normal magic square:

Properties of Magic Squares

If a square is magic, it will remain magic if it is rotated by 90°, 180°, or 270°, or if it is reflected or flipped either horizontally or vertically.

6	1	8
7	5	3
2	9	4

16	11	18
17	15	13
12	19	14

If the same number is added to or multiplied by every cell in a magic square, the square will remain magic. So, for example, if you wanted an order-3 magic square using the numbers 11 through 19, you could start with a normal 3×3 magic square (that uses the numbers 1 through 9) and add 10 to each number, giving you the square on the right. Naturally, you can subtract or divide as well.

If you can select a group of n numbers in a magic square such that there is exactly one number in each row, column, and main diagonal, you can add or subtract any number from each of those numbers, and the square will still be magic.

Unsolved Problems

One interesting unsolved problem in mathematics is determining the number of normal magic squares of a given size. It is known that there is only one normal magic square of size 3 (ignoring rotations and reflections; this is the square depicted at the top of the page), there are 880 of size 4, and 275,305,224 of size 5. For size 6 and larger, the number of normal magic squares is unknown.

Another unsolved question is whether it is possible for a 3 × 3 magic square to consist entirely of different square numbers. Any such magic square would have to satisfy pretty stringent conditions (see Magic Square of Squares on mathpages.com for more information) but no-one has proved such a square to be impossible, nor has anyone found one.

See also: Latin squares, Eulerian squares.

Sources used (see bibliography page for titles corresponding to numbers): 28, 30, 33, 34.