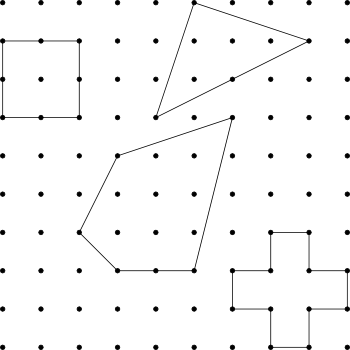
Pick's Theorem

Pick's theorem is a theorem giving the area of what are called lattice polygons, polygons all of whose vertices lie on points of a point lattice. As an example, the shapes depicted at right are all lattice polygons.

Pick's theorem gives the formula for a lattice polygon's area, A, as:

• I is the number of lattice points inside the polygon
• B is the number of lattice points on the boundary of the polygon, where the distance between each lattice point is 1 unit.

Looking at the examples at right:

• The area of the triangle is 3 + ½(5) − 1 = 4.5 square units
• The area of the square is 1 + ½(8) − 1 = 4 square units
• The area of the irregular pentagon is 8 + ½(6) − 1 = 10 square units
• The area of the 12-sided cross shape is 0 + ½(12) − 1 = 5 square units.

Pick's theorem can often come in handy when you run into such polygons, although it isn't universally useful; to take one example, an equilateral triangle could never be a lattice polygon.