Pillow-Problems: Problem #2

Problem #1 | Problem #3
For more information on this collection, see Pillow-Problems by Charles L. Dodgson (Lewis Carroll).

Problem:

In a given Triangle to place a line parallel to the base, such that the portions of sides, intercepted between it and the base, shall be together equal to the base.

Solution:

(Analysis.)

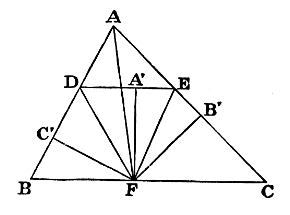
Let ABC be the Triangle, and DE the required line, so that BD + CE = BC.

From BC cut off BF equal to BD; then CF = CE.

Join DF, EF.

Now ∠BDF = ∠BFD = [by I. 29] ∠FDE;

Similarly ∠CEF = ∠FED;

∴ ∠s BDE, CED are bisected by DF, EF, and F is centre of ⊙ escribed to △ ADE.

Drop, from F, ⊥s on BD, DE, EC; then these ⊥s are equal.

Hence, if AF be joined, it bisects ∠A.

Hence construction.

(Synthesis.)

Bisect ∠A by AF: from F draw FB′, FC′, ⊥AC, AB: also draw FA′⊥BC and equal to FB′: and through A′ draw DE⊥FA′, i.e. ∥ BC. Then DE shall be line required.

∵ ∠s at A′, B′, C′ are right, and FA′ = FB′ = FC′,

∴ ∠s BDE, CED are bisected by DF, EF.

Now ∠BFD = ∠FDA′; ∴ it = ∠BDF; ∴ BF = BD;

Similarly CF = CE; ∴ BC = BD + CE.

Q.E.F.