Solutions for The Real ACT Prep Guide, 2nd Edition, practice test 2

Here are solutions for the second practice test in The Real ACT Prep Guide, 2nd Edition. While the book does provide solutions, the following solutions illustrate faster, less formal methods that may work better for you on the actual test. I haven't reprinted the questions here; see Why Do Solutions Pages Not Contain Questions? for why they aren't here.

1. • Draw a diagram: You might want to draw a simple diagram along the lines of the following:
     
   • Estimate the answer. If the restaurant rotates 180° in 45 minutes, in 60 minutes (1 hour) it will rotate somewhat more than 180°, but not significantly more.
   • Look at the answers. Only C. 240° and D. 270° appear to be reasonable.
   • Perform the required calculation. 180° × (60/45) = 240°. Therefore, the answer is C. 240°
2. If 12 vases cost $18.00, 1 vase would cost $18/12 = $1.50. Therefore, the answer is J. $1.50.
3. • Draw a diagram: It may be helpful to draw a quick sketch of a rectangle.
   • Estimate the answer. If the longer side of the apartment is 30 feet, and the shorter side is 4/6 the size, then the shorter side is probably around 20 feet. You might be able to see here that B. is the correct answer; if not, see the next step.
   • Solve the proportion. If the longer side of the apartment is 30 feet, the smaller side of the apartment must be 30 × (4/6) = 20 feet. Therefore, the answer is B. 20 feet.
4. • Read the question carefully and determine what it is asking: You are asked to find the average of $8 million, $8 million, $8 million, $9 million, and $9 million.
   • Estimate the answer: The answer is likely somewhat closer to $8 million than to $9 million. This eliminates choices J. and K.
   • Perform the calculation: (8 + 8 + 8 + 9 + 9)/5 = 8.4. Therefore the answer is H. 8.4.
5. • Try a special case: If you drive the van 2 miles, the cost will be $25.60.
   • Look at the answers: For driving the van 2 miles, choices B., C., D., and E. are all much higher than $25.60. Only A. 0.30m + 25 gives a result of $25.60. Therefore, the answer is A. 0.30m + 25.
6. • Read the question carefully and determine what it is asking: The question is asking for the measure of an angle in a quadrilateral. The four angles of a quadrilateral add to 360°, so you are looking to find 360° − 100° − 75° − 65°.
   • Perform the calculation: 360 − 100 − 75 − 65. = 360 − 100 − 140 = 360 − 240 = 120. Therefore, the answer is F. 120°.
7. • Draw a diagram: The diagram is given, but one side length is missing. Since triangle DEF is similar to triangle ABC, and the two given sides of DEF are half the corresponding sides of ABC, then the missing side must be 3.
   • Perform the required calculation: 3 + 3 + 5 = 11. Therefore, the answer must be C. 11.
8. • Read the problem and determine what it is asking: We need to find the value of (9/5) × 38 + 32 and round to the nearest degree.
   • Estimate the answer: We could quickly estimate the answer to (9/5) × 38 + 32 mentally by calculating 2 × 40 + 30. The answer to this is 110. Since we rounded up twice, this will likely be a slight overestimate, so the answer is probably closer to 100.
   • Look at the answers: The only answer anywhere near our estimate is K. 100°. Therefore, the answer has to be K. 100°.
9. • Read the question carefully: Nick needs 500 pens. The pens come in cases, each of which contain 24 × 10 = 240 pens. So, we need to find 500 ÷ 240, rounded up.
   • Estimate the answer: If the pens came in a case of 250, Nick could order 2 cases. However, the number of pens in each case is slightly smaller, so Nick will need a third case in order to get 500.
   • Look at the possible answers: Select B. 3.
10. Substitute 6 for a + b in the given equation. The result is 2(6) + 1 + 6² − 2 = 47. Therefore, the answer is K. 47.
11. If one hamburger and one soft drink cost $2.10 and an additional hamburger brings the cost to $3.50, then that second hamburger costs $1.40. If one hamburger and one soft drink cost $2.10, and the hamburger costs $1.40, then the drink must cost $0.70. Therefore, the answer is C. $0.70.
12. Solution 1: Solve the equation:
    12x = −8(10 − x)
    12x = −80 + 8x 4x = −80
    x = −20
    Therefore, the answer is K. −20.
    Solution 2: Guess and check: Test each of the given answers, starting with the integer solutions (since the arithmetic will be simpler). If you are very observant, you'll notice you don't have to check G., H., and J. at all; they result in the left-hand side of the equation being positive and the right negative, so they can't be right. After a few guesses, you should find that the answer is K. −20.
13. • Draw a diagram: You might find it helpful here to draw a quick sketch.
    • Estimate the answer: The countertop is 6 tiles wide by around 15 tiles wide, or around 90 tiles.
    • Look at the answers: B. 88 and C. 96 are within range of our estimate.
    • Perform the required calculation: The number of tiles required is (24/4)(64/4) = 96. Therefore, the answer is C. 96.
14. • Read the question carefully and determine what it is asking: You are, in essence, being asked which of the triangles with given angle measurements is isosceles.
    • Guess and check: If two of the triangle's angles are 20° and 40°, then the third must be 120°, which doesn't make for an isosceles triangle. So, F. is incorrect. Repeat the process until you get to the correct answer, H. 40°, 100°.
15. • Draw a diagram: It may be helpful to draw a quick sketch of the triangle in question.
    • Estimate the answer: The other two sides have a total length of 50, so the largest side must be larger than 25. However, since the sides are in the ratio 2:3, it can't be too much larger than 25, say around 30.
    • Look at the answers: The only answer that makes sense is C. 30. Select that answer.
16. • Draw a diagram: Draw a sketch of the graph, which might look something like:
      
    • Estimate the answer: Looking at the diagram, the answer must be greater than 2 and less than 6. Probably the answer is around 4.
    • Look at the possible answers: The only answer greater than 2 and less than 6 is H. 4. Therefore, this must be the answer.
17. • Estimate the answer: While the diagram may not be drawn to scale, it appears to be reasonably close; x appears to be somewhere around 30.
    • Draw a diagram: The diagram is already given. However, since the two transversals intersect a pair of parallel lines and the diagram contains a triangle (whose angles add to 180°, we can fill in more of the diagram:
      
      Having filled in some numbers, it can be seen that x = 35. Select answer C.
18. The quickest way to solve this problem is to notice that the depth of the first pond is being reduced ½ cm/week relative to the depth of the second pond. Since the first pond is 20 cm deeper than the second, it will take 20 cm ÷ ½ cm/week = 40 weeks for the ponds to have the same depth. Therefore, the answer is H. 40.
19. E. is a quadratic equation, not a linear equation like the other possibilities. Therefore, the answer is E. x² + y = 5.
20. Look at the possible answers: The answers all contain some combination of 12 and 13. Relative to A, 12 is the opposite side and 13 is the hypotenuse. The sine is equal to opposite/hypotenuse, which in this case is 12/13. Therefore, the correct answer is G. sin A = 12/13.
21. Break the problem up: First, determine the slope of 7x + 9y = 6. The easiest way is to write the equation in slope-intercept form:
    7x + 9y = 6 9y = −7x + 6 y = −(7/9)x + 2/3 So, the slope of the line is −7/9. Therefore, this must be the slope of any parallel line. Select B. −7/9.
22. Solution 1:
    • Guess and check: It probably makes sense to start with the middle answer (40) to give you a sense of whether the answer is higher or lower than 40; also, as there's a 40 in the denominator, it may make the mathematics easier:
      y = 3(40² + 10(40))/40
      y = 3(40 + 10)
      y = 150
      As it turns out, 40 miles per hour is the maximum possible speed. Therefore, the answer is H. 40.
    Solution 2:
    • Draw a diagram: It's probably impractical to draw the graph by hand. However, if you have a graphing calculator, plot the function given. If you examine the graph, you'll notice that the y-value for x = 30 is around 100, for x = 40 y is around 150, and for x = 50 y is about 200. Therefore, the answer is H. 40.
    Solution 3: You can substitute 150 for y and solve the resulting quadratic equation:
    150 = 3(x² + 10x)/40
    2000 = x² + 10x
    x² + 10x − 2000 = 0
    (x + 50)(x − 40) = 0
    x = −50 or x = 40
    Of course, only the positive solution is relevant here. So, the answer is H. 40.
23. • Break the problem up: g(4) = √4 = 2. f(1) = 1² + 1 + 5 = 7. g(4)/f(1) = 2/7. So, the answer is A. 2/7.
24. • Calculate or estimate the answer: You may know that the way to calculate the number of combinations in this scenario is to multiply the two numbers together. So, the answer would be 125 × 100 = 12,500. Otherwise, it may be possible to estimate the answer. If there were 1 junior and 100 seniors, there would be 100 possible combinations. If there were 2 juniors and 100 seniors, there would be 200 possible combinations. It may be helpful to draw a diagram. So, with 125 juniors and 100 seniors, it seems reasonable that there are 12,500 combinations.
    • Look at the possible answers: The answer K. 12,500 matches the estimate. No other answer is even close. So, the answer is K. 12,500.
25. • Draw a diagram: Your diagram might look something like the following:
      
      Drawing the diagram, you can see that this is a problem relating to similar triangles.
    • Estimate the answer: The answer is definitely less than 100, perhaps 2/5 of 100, or somewhere around 40.
    • Look at the answers: The only reasonable answer is C. 40.
26. Guess and check: Start with one of the more extreme values, say F. −10. If t = −10, then the inequality becomes:
    |−10 − 24| ≤ 30
    |− 34| ≤ 30
    34 ≤ 30
    Is 34 ≤ 30? No. Therefore, the answer must be F. −10.
27. Solution 1:
    • Translate the sentence into an equation: The equation corresponding to the given sentence is:
      15 − 5n < 0
      Note that you have to read the sentence carefully; it reads "subtracted from."
    • Solve the equation:
      15 < 5n
      n > 3
      Select D. All n > 3.
    Solution 2:
    • Translate the sentence into an equation, as above.
    • Try a special case: Try one or more special cases until you eliminate all of the answer choices but one. For example, if you try n = 7, the inequality is true. The only corresponding choice is D. All n > 3.
28. Evaluate the expression, being careful with signs:
      (x² − 4x + 3) − (3x² − 4x − 3)
    = x² − 4x + 3 − 3x² + 4x + 3
    = −2x² + 6
    Therefore, the answer is J. −2x² + 6.
29. • Try a special case: Say that the 9 items are, say, 3, 4, 5, 6, 7, 8, 9, 10, and 11, and that the four items added to the data set are 1, 2, 12, and 13. In this case, the median of the original data set is 7, and the median of the new data set is also 7.
    • Look at the possible answers: The only answer that is correct in regard to the special case above is B.. Therefore, the answer is B. It is the same as the original median.
30. • Estimate the answer: The area of the unshaded region is π(5)² = 25π. The shaded area is definitely larger than the unshaded area; it appears to be more than twice the unshaded area. Perhaps it is around 3 times the area of the unshaded area, or 75π.
    • Look at the possible answers: The only answer that is larger than the unshaded area is K. 75π. Therefore, select K. 75π.
31. Solution 1: You may remember that a 30°-60°-90° triangle is a special triangle with side lengths in the ratio of 1:√3:2. The only matching answer is E. 1, √3, 2.
    Solution 2:
    • Draw a diagram: It may be helpful to draw a diagram for this question.
    • Look at the answers: In all of the answers, the shortest side is 1. This side must be opposite the smallest angle (the 30° one). Add that information to the diagram, and label the unknown side lengths x and y:
    • Set up and solve the equation: To find the length of the hypotenuse y, we could solve the following equation:
      1/y = sin 30°
      y = 2
      The only answer with a side length of 2 is E.. Therefore, the answer is E. 1, √3, 2. Alternately, we could have solved 1/x = tan 30°, and found x to be √3, and found the hypotenuse using the Pythagorean theorem.
    Solution 3: If you don't remember either special triangles or trigonometry, the problem is still possible to solve if you think about it logically.
    • Draw a diagram: Draw a diagram similar to that in solution 2. Then, flip the triangle over as shown below.
      
      This forms one big triangle. You can see that the triangle has three 60° angles, and so it must be an equilateral triangle. Since the length of one of the sides is 1 + 1 = 2, the length of the other two sides must also be 2. Therefore, one of the sides of the 30°-60°-90° triangle must be 2.
    • Look at the answers: The only answer containing side lengths of 1 and 2 is E. 1, √3, 2. Select that answer.
32. • Read the question carefully and determine what it is asking: You are asked to find 0.005(20)² − 2(20) + 200.
    • Estimate the answer: The last two terms sum to 160, and the first term appears to be small. So, the answer is slightly greater than 160, probably somewhere around 165.
    • Look at the answers: All of the answers, except for F., are in the range of our estimate.
    • Perform the calculation: 0.005(20)² − 2(20) + 200 = 162. Therefore, the answer is G. 162.
33. • Read the question carefully and determine what it is asking: You are asked to find the hypotenuse of a right-angled triangle whose legs are both 200.
    • Estimate the answer: The length of the line must be greater than 200, as it has to be longer than either leg. It must be less than 400 due to the triangle inequality. Perhaps the answer lies somewhere around 300.
    • Look at the answers: The only answer within our estimated range is D. 283. Select that answer.
34. • Estimate the answer: The area is definitely less than 20,000 square units; perhaps it's around 17,000 square units or so.
    • Look at the answers: F. and G. are the only answers corresponding to our estimate. Looking at the diagram, the shaded are and the curve lie under FG, so the correct answer is F. less than 20,000 square units, because the curve lies under FG.
35. • Draw a diagram: The diagram is given, and the equation to use is given, but we need to map the information in the diagram onto the equation. We can do this if we label the lighthouse as C and the other two vertices as A and B (which one is which doesn't matter).
    • Look at the possible answers: The answers are not simplified, so we just need to set the equation up. You may be able to see what the answer is already. If not, go to the next step.
    • Solve the equation:
      c² = (4.2)² + (5.0)² − 2 · 4.2 · 5.0 cos 5°
      c = √(4.2)² + (5.0)² − 2 · 4.2 · 5.0 cos 5°
      Therefore, the answer is B. √(4.2)² + (5.0)² − 2 · 4.2 · 5.0 cos 5°
36. Solution 1: Substitute a³ = b in b² = c. This results in (a³)² = c, or a⁶ = c. Therefore, the answer is F. c = a⁶. Solution 2:
    • Try a special case: Say that a = 2. then b = 8, and c = 64.
    • Look at the possible answers. The only one of the five answers that is correct when a = 2 and c = 64 is F. c = a⁶. Select this answer.
37. Look at the possible answers: The easiest way to solve this problem is to notice that D. and E. can't both be correct. The sequence in question is an arithmetic sequence, so the terms have a common difference, not a common ratio. Therefore, the answer is E. The common ratio of consecutive terms is −5.
38. There are several ways to do this problem. You may remember that the area of a parallelogram is bh. Alternately, if you remember that the area of a triangle is ½bh, you can divide the parallelogram into two triangles, or two triangles and a rectangle. Alternately, you might notice that the area of the parallelogram is equal to a rectangle with vertices (0,0), (10,0), (10,6), and (0,6). Either way, you should get G. 60.
39. • Read the question carefully and understand what it is asking: You are asked to find 1.5 × 10⁻⁵ × 100.
    • Estimate or calculate the answer: Actually, the required calculation is pretty straightforward (assuming you remember the laws of exponents); 10⁻⁵ × 100 = 10⁻³
    • Look at the possible answers: The calculation corresponds to D. 10⁻³.
40. • Estimate the answer: Based on what you know about square roots, you might think the answer should be 2 or 3, or perhaps it might vary.
    • Look at the possible answers: Our estimate might fit with three answers: G. 2, H. 3, and K. Cannot be determined from the given information.
    • Perform the calculation: The smallest number in the range we're looking at is 1,000. On your calculator, evaluate √1,000. The result is, to two decimal places, around 31.62. The largest number is 9,999. On your calculator evaluate √9,999. The result is, to two decimal places, 99.99. So, if any number between 1,000 and 9,999 is a perfect square, its square root must be between 32 and 99. Therefore, the answer is G. 2.
41. Solution 1:
    • Perform the calculation: (½x − y)² = ¼x² −2(½)xy + y². Therefore, the answer is B. (¼x² − xy + y²).
    Solution 2:
    • Try a special case: Assume that x = 2 and y = 1. Then the expression equals 0.
    • Look at the possible answers: If x = 2 and y = 1, then A. and D. are definitely greater than zero, so they can't be correct. The value of C. is 1, and the value of E. is 3. The value of B. is 0, so the correct answer has to be B. (¼x² − xy + y²).
42. The actual arithmetic is straightforward, but you do need to understand matrix multiplication. The correct answer is F.
43. • Read the question carefully and understand what it is asking: You are asked to find the value of 2x° based on the information in the diagram.
    • Estimate the answer: Based on the diagram, 4x + 6 + 2x = 180. So, if 6x is somewhere around 180°, then x is somewhere around 30° and 2x is somewhere around 60°.
    • Look at the possible answers: The only answer anywhere near our estimate is D. 58°. Select this answer.
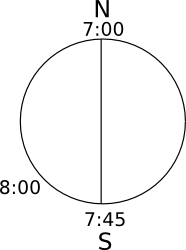
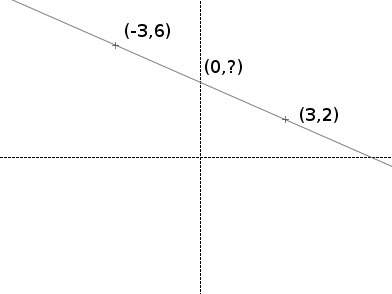
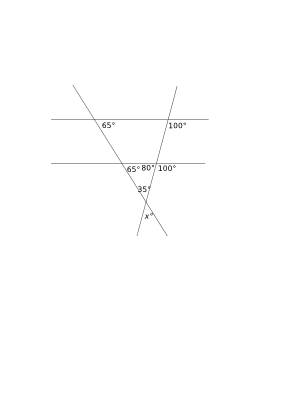
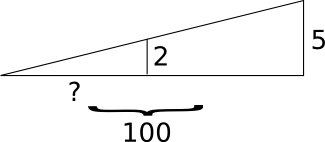
44. • List all of the numbers between 30 and 50:
      30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50
    • Cross out all of the numbers divisible by 2:
      30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50
    • Cross out all of the numbers divisible by 3:
      30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50
    • Cross out all of the numbers divisible by 5 (we don't need to worry about numbers divisible by 4, since they are also divisible by 2):
      30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50
    • Cross out all of the numbers divisible by 7:
      30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50
    • We only have to check numbers less than √50, so we're done. The remaining numbers are 31, 37, 41, 43, 47. Therefore, the answer is G. 5.
45. This is a straightforward question, as long as you remember that the tangent is opposite/adjacent, so cotangent must be adjacent/opposite. So:
    cot A = √4 - x²/x.
    Therefore, the answer is E. √4 - x²/x.
46. • Read the question carefully and determine what it is asking.
    • Draw a diagram: Draw 10 "booths". Each booth must have at least one person in it, so draw one "person" in each. There are now 10 people remaining, and they could fill three booths with one person left over. Therefore, the answer is J. 3.
47. Try a special case: The sum of the bases of the two triangles is 4. Assume that the left triangle has a base of 2, and the right triangle has a base of 2 (you could also use other numbers that sum to 4, such as 3 and 1). Each triangle has an area of ½(3)(2) = 3, so the sum is 6. Therefore, the answer must be B. 6.
48. • Estimate the answer: ABCD has a perimeter of 48. The perimeter of EFGH is somewhat smaller; you might estimate it to be around 30 or so.
    • Look at the answers: H., J., and K. are not correct since they're greater than 48, but we have to decide between F. and G.
    • Draw a diagram: If AB = 12, AE = 6 and AH = 6. The Pythagorean theorem can be used to find EH. It is 6√2. Therefore, the perimeter of EFGH is G. 24√2.
49. Solution 1:
    • Try a special case: Say that x = 2. Then I is equal to 2, II is equal to 2, and III is equal to −2.
    • Look at the answers: Since III doesn't equal either I or II, then B., C., and D. must not be incorrect. We still need to decide between A. I and II only and E. None of the expressions are equivalent.
    • Try another special case: Try one or more special cases until you are satisfied that the answer is A. I and II only.
    Solution 2: Graph the three equations on your graphing calculator. You should be able to see that I and II are the same, but III is different. Therefore, the answer is A. I and II only.
50. • Draw a diagram: The diagram is already given; however, it is useful to fill in some of the angles. While we don't know the exact values, it may be useful to give one of the angles, say ACB, a value of x and go from there:
      
    • Look at the answers: F. is justifiable, since both lines meet AD at right angles. You are given that angle CED is a right angle, so G. is justified. The two vertical angles at C are equal, so H. is justified. Based on the angle measurements we've written in the diagram, J. is also justified. However, we don't have any information about the lengths of the lines, so the answer must be K. CE is congruent to ED.
51. • Draw a diagram: It can be helpful to notice that the perimeter of the shape in question is the same as the perimeter of:
      
    • Calculate the answer: The perimeter of the modified shape is 2(4 + 3) = 14, so that must be the perimeter of the original shape.
    • Look at the possible answers: The correct answer is D. 14.
52. • Estimate the answer: The area of the rectangle is 48 square inches, and the area of the circle seems to be somewhat around 1.5 times that or so. So, the area seems to be around 75 or so.
    • Look at the possible answers: The only answer that appears to be in range is H. 25π. G. is about the same size as the area of the rectangle, and J. is over 150, three times the size of the rectangle. Therefore, the answer is H. 25π.
    • If you aren't convinced that you can eliminate G. or J., you can work backwards:
      • To find the area of the circle, you need the radius.
      • You could find the radius if you had the diameter.
      • The diameter is the same as the diagonal of the rectangle.
      • You can find the diagonal of the rectangle using the Pythagorean theorem.
      Putting all that together, the diagonal of the rectangle is 10, the radius is 5, and the answer is H. 25π.
53. • Read the question and understand what it is asking: You are asked to find the sum of the first 20 terms of the arithmetic series 24 + 29 + 34 + ...
    • Estimate the answer: Marshall made 24 calls on his first day. Since the number of calls goes up by 5 each day, he probably made around 120 by day 20. Say that he made around 70 calls on average during each of the 20 days. Then he would have made around 70 × 20 = 1,400 calls in total.
    • Look at the answers: D. 1,430 looks promising, but E. 1,530 is also close, so we'll need to perform the calculation.
    • Perform the required calculation: You can add the first 20 terms of the arithmetic series on your calculator. However, it's faster if you remember the formula for the sum of an arithmetic sequence, which is (n/2)(2a + (n − 1)d), where a is the first term (24) and d is the difference between terms (5). The sum of the first 20 terms is:
      (20/2)(2(24) + (19)(5)) = 1,430
      Select D. 1,430.
54. Look at the answers: You are looking for a graph of a function. G., H., and J. are not functions (they fail the vertical line test). The function must contain part of an upwards-facing parabola, so that eliminates F. So, the correct answer must be K.
55. Solution 1:
    • Using your calculator, evaluate cos⁻¹(-0.385). The value should be, to three decimal places, 1.966.
    • Look at the answers: Since π is a bit larger than 3, then π/2 is a bit larger than 1.5, and 2π/3 is a bit larger than 2 (or, since you already have your calculator out, you can use it to find exact values for these). Therefore, the answer must be D. π/2 ≤ θ < 2π/3.
56. Solution 1:
    • Perform the required calculation: If x = 6a and x = −3b are the solutions of a quadratic equation, then that equation must be (x − 6a)(x + 3b) = 0. Expand the left-hand side and you get x² + x(3b − 6a) − 18ab = 0. Therefore, the correct answer is J. x² + x(3b − 6a) − 18ab = 0.
    Solution 2:
    • Work backwards: Try factoring each of the answers to see which left-hand side of the equation is equivalent to (x − 6a)(x + 3b). The correct answer is J. x² + x(3b − 6a) − 18ab = 0.
57. Solution 1: You may remember that the equation of a circle centred on (a, b) with radius r is (x − a)² + (y − b)² = r². This circle is centred on (3,3) and it has radius 3. So, the answer must be A. (x − 3)² + (y − 3)² = 9 (don't forget that the right-hand side is r squared). Solution 2:
    • Try a special case: It appears that one point on the circle is (3,0).
    • Look at the possible answers: Substituting x = 3, y = 0 into the five equations, equation A. is the only one that works. Therefore the answer must be A. (x − 3)² + (y − 3)² = 9.
58. • Try a special case: Say that the length of Pendulum 1 is 18 feet (why 18? 18 is divisible by three of the answers 3, 6, 9, so hopefully the arithmetic will be easier with this assumption). Then, for the first pendulum:
      t = 2π√18/32
      t = 2π√9/16
      t = 2&pi(¾)
      t = 3π/2
      So, for the second pendulum, t = π/2, and we get:
      π/2 = 2π√L/32
      1/4 = √L/32
      1/16 = L/32
      L = 2
      
      So, the first pendulum is 9 times the length of the second pendulum.
    • Look at the possible answers: Select J. 9.
59. Solution 1:
    • Try a special case: Say that a = 10, x = 1, and y = 10. Then s = 0, t = 1, and log_a(xy)² = log₁₀100 = 2.
    • Look at the possible answers: In the special case above, answers C., D., and E. are all 0. Answer B. is 1. Only answer A. gives the expected value of 2. Therefore, the answer is A. 2(s + t).
    Solution 2: Simplify the expression:
      log_a(xy)²
    = 2 log_a(xy)
    = 2(log_ax + log_ay)
    = 2(s + t)
    Therefore, the answer is A. 2(s + t).
60. • Estimate the answer: The answer is probably somewhere around (10 + 20)% = 30%. There are two values in that range, F. 32% and G. 30%. This being question 60, we probably shouldn't assume that the answer is as simple as G. 30 without further calculation.
    • Try a special case: If Jennifer's best long jump distance in 1990 was 100 feet, then her distance in 1991 is 100 × 110% = 110 feet. Then, her distance in 1992 is 132 feet (110 × 120%). This represents an increase of (132 - 100)/100 × 100% = 32%. Therefore, the answer is F. 32%.

Previous test in this book: test 1.