The Baseball Diamond

Briggs Stadium, Detroit, Mich. Postcard ca. 1942.

In a certain baseball diamond, the distance from home plate to the foul pole in left field is 310 feet. The distance from home plate to the foul pole in right field is 330 feet. The distance from home plate to centre field is 400 feet. What is the area inside the foul lines in the baseball stadium if:

1. The outfield wall runs along a straight line from left field to centre field and along another straight line from centre field to right field?
2. The outfield wall is the arc of a circle?

I haven't yet given the answer here, although I may in the future.

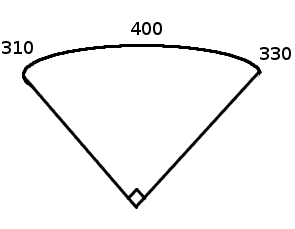The first problem can be solved using geometry, by breaking up the diamond into shapes that are easier to work with. The second problem requires more advanced mathematics (e.g. calculus) as well as some problem solving skills, and a fair bit of patience; the problem hasn't been constructed so as to be computationally easy. If you have questions about the problem, you can contact me.

If you're interested in baseball, you may also be interested in the problems about baseball cards.