Pillow-Problems: Problem #28

Problem #27 | Problem #29
For more information on this collection, see Pillow-Problems by Charles L. Dodgson (Lewis Carroll).

Problem:

If the sides of a given Triangle, taken cyclically, be divided in extreme and mean ratio; and if the points be joined: find the ratio which the area of the Triangle, so formed, has to the area of a given Triangle.

Answer:

7 − 3√5.

Solution:

Let ABC be the given Triangle; and let its sides be divided internally at A′, B′, C′, in extreme and mean ratio.

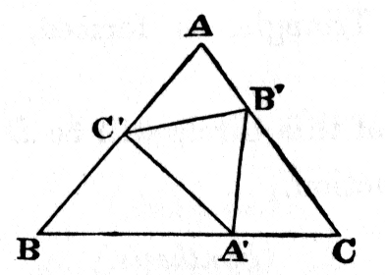
And let M be the area of ABC.

Let BA′ = x; then x² = a · (a − x);

i.e. x² + ax − a² = 0;

∴ x =

(−a ± a√5)/

(2)

=

(a)/

(2)

· (√5 − 1), the other sign being excluded by the terms of the question.

Then area of Triangle AB′C′

Similarly for BC′A′ and CA′B′.

Hence the sume of these 3 Triangles = 3 · (√5 − 2) · M, and area of Triangle A′BC′ = (7 − 3√5) · M.

Q.E.F.