The following is as given in
Sir Thomas L. Heath's translation, which can be found in the book
The Thirteen Books of The Elements, Vol. 1.
| Book I | Book II | Book IX |
|---|---|---|
| Definitions, Postulates, and Common Notions | Definitions | Proposition 20 |
| Proposition 1, Proposition 3, | Proposition 14 | Proposition 36 |
| Proposition 5, Proposition 6, | ||
| Proposition 29, Proposition 47 |
To construct a square equal to a given rectilineal figure.
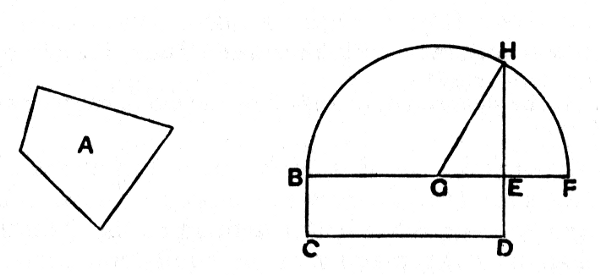
Let A be the given rectilineal figure;
thus it is required to construct a square equal to the rectilineal figure A.
For let there be constructed the rectangular parallelogram BD equal to the rectilineal figure A. [I. 45]
Then, if BE is equal to ED, that which was enjoined will have been done; for a square BD has been constructed equal to the rectilineal figure A.
But, if not, one of the straight lines BE, ED is greater.
Let BE be greater, and let it be produced to F;
let EF be made equal to ED, and let BF be bisected at G.
With centre G and distance one of the straight lines GB, GF let the semicircle BHF be described; let DE be produced to H, and let GH be joined.
Then, since the straight line BF has been cut into equal segments at G, and into unequal segments at E,
the rectangle contained by BE, EF together with the square on EG is equal to the square on GF.
But GF is equal to GH;
therefore the rectangle BE, EF together with the square on GE is equal to the square on GH.
But the squares on HE, EG are equal to the square on GH;
[I. 47]
therefore the rectangle BE, EF together with the square on GE is equal to the squares on HE, EG.
Let the square on GEbe subtracted from each;
therefore the rectangle contained by BE, EF which remains is equal to the square on EH.
But the rectangle BE, EF is BD, for EF is equal to ED;
therefore the parallelogram BD is equal to the square on HE.
And BD is equal to the rectilineal figure A.
Therefore the rectilineal figure A is also equal to the square which can be described on EH.
Therefore a square, namely that which can be described on EH, has been constructed equal to the given rectilineal figure A.
Q.E.F.